Trabalho de Física – Prof° Felipe Martins
Alunas: Tatiele Acosta
e Ane Caroline – 3° Ano
ESTUDO DO ESPELHO PLANO
Desenvolvimento
Espelho
plano
Um espelho plano é aquele em que a
superfície de reflexão é totalmente plana.
Os espelhos planos têm utilidades
bastante diversificadas, desde as domésticas até como componentes de
sofisticados instrumentos ópticos.
Representa-se um espelho plano por:
As principais propriedades de um
espelho plano são a simetria entre os pontos objeto e imagem e que a maior
parte da reflexão que acontece é regular.
Construção das imagens em um espelho
plano
Para se determinar a imagem em um
espelho plano basta imaginarmos que o observador vê um objeto que parece estar
atrás do espelho, isto ocorre, pois o prolongamento do raio refletido passa por
um ponto imagem virtual (PIV), "atrás" do espelho.
Nos espelhos planos, o objeto e a
respectiva imagem têm sempre naturezas opostas, ou seja, quando um é real o
outro deve ser virtual, portanto, para se obtiver geometricamente a imagem de
um objeto pontual, basta traçar por ele, através do espelho, uma reta e marcar
simetricamente o ponto imagem.
Translação de um espelho plano
Considerando a figura:
A parte superior do desenho mostra uma
pessoa a uma distância d1 do espelho, logo a imagem
aparece a uma distância d1 em relação ao espelho.
Na parte inferior da figura, o espelho
é transladado ℓ para a direita, fazendo com que o
observador esteja a uma distância d2 do espelho, fazendo com que a
imagem seja deslocada x para a direita.
Pelo desenho podemos ver que:
Que pode ser reescrito como:
Mas pela figura, podemos ver que:
ℓ = d2 – d1
Logo:
Assim pode-se concluir que sempre que
um espelho é transladado paralelamente a si mesmo, a imagem de um objeto fixo
sofre translação no mesmo sentido do espelho, mas com comprimento equivalente
ao dobro do comprimento da translação do espelho.
Se utilizarmos esta equação, e medirmos
a sua taxa de variação em um intervalo de tempo, podemos escrever a velocidade
de translação do espelho e da imagem da seguinte forma:
Ou seja, a velocidade de deslocamento
da imagem é igual ao dobro da velocidade de deslocamento do espelho.
Quando o observador também se desloca,
a velocidade ao ser considerada é a velocidade relativa entre o observador e o
espelho, ao invés da velocidade de translação do espelho, ou seja:
Associação de dois espelhos planos
Dois espelhos planos podem ser associados, com as superfícies
refletoras se defrontando e formando um ângulo α entre
si, com valores entre 0° e 180°.
Por razões de simetria, o ponto objeto e os pontos imagem ficam
situados sobre uma circunferência.
Para se calcular o número de imagens que serão vistas na
associação usa-se a fórmula:
Sendo α o
ângulo formado entre os espelhos.
Por exemplo, quando os espelhos encontram-se perpendicularmente,
ou seja, α =90°:
Portanto, nesta configuração são vistas 3 pontos imagem.
Espelhos
esféricos
Chamamos espelho esférico qualquer calota esférica que seja polida e
possua alto poder de reflexão.
É fácil observar-se que a esfera da
qual a calota acima faz parte tem duas faces, uma interna e outra externa.
Quando a superfície refletiva considerada for à interna, o espelho é
chamado côncavo, já nos
casos onde a face refletiva é a externa o espelho é chamado convexo.
Reflexão da luz em espelhos esféricos
Assim como para espelhos planos, as duas leis da reflexão também são obedecidas nos espelhos esféricos, ou seja, os ângulos de incidência e reflexão são iguais, e os raios incididos, refletidos e a reta normal ao ponto incidido.
Aspectos geométricos dos espelhos
esféricos
Para o estudo dos espelhos esféricos é
útil o conhecimento dos elementos que os compõe, esquematizados na figura
abaixo:
- C é o centro da
esfera;
- V é o vértice da
calota;
- O eixo que passa pelo centro
e pelo vértice da calota é chamado eixo principal.
- As demais retas que cruzam o
centro da esfera são chamadas eixos
secundários.
- O ângulo α, que mede a distância angular
entre os dois eixos secundários que cruzam os dois pontos mais externos da
calota, é a abertura do
espelho.
- O raio da esfera R que
origina a calota é chamado raios
de curvatura do espelho.
Um sistema óptico que consegue conjugar
a um ponto objeto, um único ponto como imagem é dito estigmático. Os espelhos
esféricos normalmente não são estigmáticos, nem aplanéticos ou ortoscópicos,
como os espelhos planos.
No entanto, espelhos esféricos só são estigmáticos para os raios que incidem próximos do seu vértice V e com uma pequena inclinação em relação ao eixo principal. Um espelho com essas propriedades é conhecido como espelho de Gauss.
Um espelho que não satisfaz as condições de Gauss (incidência próxima do vértice e pequena inclinação em relação ao eixo principal) é dito astigmático. Um espelho astigmático conjuga a um ponto uma imagem parecendo uma mancha.
No entanto, espelhos esféricos só são estigmáticos para os raios que incidem próximos do seu vértice V e com uma pequena inclinação em relação ao eixo principal. Um espelho com essas propriedades é conhecido como espelho de Gauss.
Um espelho que não satisfaz as condições de Gauss (incidência próxima do vértice e pequena inclinação em relação ao eixo principal) é dito astigmático. Um espelho astigmático conjuga a um ponto uma imagem parecendo uma mancha.
Focos dos espelhos esféricos
Para os espelhos côncavos de Gauss pode ser
verificar que todos os raios luminosos que incidirem ao longo de uma direção
paralela ao eixo secundário passa por (ou convergem para) um mesmo ponto F - o
foco principal do espelho.
No caso dos espelhos convexos é a
continuação do raio refletido é que passa pelo foco. Tudo se passa como se os
raios refletidos se originassem do foco.
Determinação
de imagens
Analisando objetos diante de um espelho esférico, em posição perpendicular ao eixo principal do espelho podemos chegar a algumas conclusões importantes.
Um objeto pode ser real ou virtual. No caso dos
espelhos, dizemos que o objeto é virtual se ele se encontra “atrás” do espelho.
No caso de espelhos esféricos a imagem de um objeto pode ser maior,
menor ou igual ao tamanho do objeto. A imagem pode
ainda aparecer invertida em relação ao objeto. Se não houver
sua inversão dizemos que ela é direita.
Equação fundamental dos espelhos esféricos
Dadas à distância focal e posição do objeto é possível determinar, analiticamente, a posição da imagem. Através da equação de Gauss, que é expressa por:














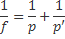
Nenhum comentário:
Postar um comentário